Cluster k medias

Descripción de la técnica

Si como antes mencionábamos, los criterios jerárquicos tenía como misión generar un único grupo (aglomerativo) a partir de n elementos, los criterios no jerárquicos tiene como misión establecer k particiones a partir de los n elementos en los que se den las máximas generales de mayor diferenciación intergrupo y menor intragrupo sin condición de jerarquía entre las mismas. Se trabaja directamente sobre los elementos y permiten que la muestra sea mucho más elevada, dado que no es necesaria la matriz de distancias total.

Es muy importante destacar que en este tipo de procesos se produce los que se denomina reasignación del elemento a clasificar que a medida que se producen iteraciones puede ir variando de grupo para ajustarse más a otra partición más semejante. El método más habitual de cálculo de este tipo es el que dispone BarbWin, el K-medias.

Una vez obtenidos los cálculos, el análisis debe finalizar intentando explicar la composición de malos grupos en dos direcciones. La primera de ellas debe llevar al investigador a intentar comprender y verificar las diferencias entre los grupos, nominando los mismos en función de las características más diferenciadoras. La segunda de ellas tratando de verificar si esos grupos revelan también diferencias en las variables de perfil de la muestra, identificando datos de clasificación relevantes en ellos. Quedaría por último, analizar la trascendencia del grupo ante el resto de preguntas del trabajo de investigación, pensando en que la respuesta de los grupos puede ser diferenciada ante cualquier cuestión de nuestro trabajo.

Grado de utilización en la práctica

Muy utilizado. Es el análisis tipo cuando se trata de clasificar objetos. Al igual que en el cluster jerárquico, se suele utilizar con variables de tipo numérico métrico y para ser comparadas es preferible que las variables estén en la misma escala, aunque no es requisito para el análisis. También, se pueden utilizar variables artificiales para realizar el análisis. El software con el que trabajamos, BarbWin, realiza esta operativa directamente si en el análisis se incluyen variables nominales o múltiples.

Información ofrecida por un análisis de cluster

Clusters iniciales	Se muestran los centro de cluster de las variables en los grupos que se ha decidido comenzar a crear
Descriptivos de las variables	Medias y desviaciones de los grupos iniciales según criterio elegido
Matriz de correlaciones de Pearson	Análisis visual de las correlaciones entre grupos iniciales
Distribución de casos por cluster	Muestra identificados para el número de relación con la variable qué casos caen en cada cluster
Informes de cluster	Distancia de cada caso al centro del cluster, medias de los grupos, composición de los mismos, distancia promedio al centro del grupo
Análisis de varianza final	Verifica la existencia de significatividad en las diferencias entre los clusters o grupos.
Distancias entre centro de clusters	Indicativo de la dispersión del grupo
Clusters finales	Medias de los clusters en cada grupo.

Proceso y opciones de cálculo

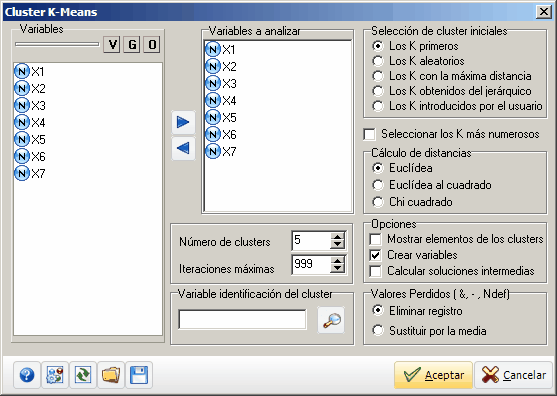
clip0337

Diálogo de cluster k-medias

•	Selección de variables, de tipo numérico, nominal o múltiple.

•	Selección del criterio de partida, k elementos (número de particiones o grupos deseados) de forma distinta:

•	los k primeros que encuentra en la matriz,

•	los k más distantes (cálculo de matriz de distancias),

•	los k aleatorios, los k introducidos por el usuario.

•	La medida inicial del centroide es la media aritmética.

•	Selección de la medida de distancia, Para el cálculo inicial de elementos y para la posterior inclusión o reasignación del elemento en la partición.

Proceso

Fichero Datos para cluster.gbw

Órdenes Seleccionar variables de X1 a X7

Opciones K con máxima distancia, Distancia Euclídea, Informe de contenido de clusters, Crear variable (GRUPO_5)

Análisis de 5 clusters

Cálculo de distancias: distancia euclídea al cuadrado

Método de inicio en el cluster: comenzar con los 5 más distantes

X1 Velocidad de entrega

X2 Nivel de precios

X3 Flexibilidad en precios

X4 Imagen del fabricante

X5 Nivel de servicio

X6 Imagen del personal de ventas

X7 Calidad del producto

Clusters iniciales

	X1	X2	X3	X4	X5	X6	X7
1	6,00000	0,90000	9,60000	7,80000	3,40000	4,60000	4,50000
2	2,60000	3,00000	8,50000	6,00000	2,80000	2,80000	6,80000
3	2,50000	1,80000	9,00000	5,00000	2,20000	3,00000	6,00000
4	3,10000	2,20000	6,70000	6,80000	2,60000	2,90000	8,40000
5	2,00000	2,80000	5,20000	5,00000	2,40000	2,70000	8,40000

Número de sujetos a clasificar: 100

Número de variables observadas: 7

Número de clusters: 5

Descriptivos de las variables

Nombre	Media	Desviación típica	Coeficiente variación
X1	3,515	1,314	37,386
X2	2,364	1,190	50,324
X3	7,894	1,380	17,476
X4	5,278	1,119	21,196
X5	2,946	0,812	27,553
X6	2,665	0,767	28,780
X7	6,971	1,577	22,627

Matriz de correlaciones

Nombre	X1	X2	X3	X4	X5	X6	X7
X1	1,00000	-0,34923	0,50930	0,05042	0,56306	0,07712	-0,48263
X2	-0,34923	1,00000	-0,48721	0,28373	0,48594	0,18624	0,46975
X3	0,50930	-0,48721	1,00000	-0,07784	0,11509	-0,03432	-0,44811
X4	0,05042	0,28373	-0,07784	1,00000	0,32322	0,75944	0,17453
X5	0,56306	0,48594	0,11509	0,32322	1,00000	0,17525	-0,08761
X6	0,07712	0,18624	-0,03432	0,75944	0,17525	1,00000	0,17729
X7	-0,48263	0,46975	-0,44811	0,17453	-0,08761	0,17729	1,00000

Distribución e informe de casos por cluster

Cluster	Casos	Porcentaje
1	17	17,00
2	25	25,00
3	33	33,00
4	6	6,00
5	19	19,00

Informe del cluster 1 de una solución de 5 clusters - Contiene 17 Casos ( 17,00% sobre el total)

Caso	Distancia al centro
5	1,08055
7	0,48255
9	0,35479
14	0,32003
15	0,26623
19	0,10209
20	0,26623
26	0,45263
28	0,10572
33	0,47084
42	1,06454
58	0,33562
62	0,52834
67	0,22680
76	0,61214
90	0,25546
97	0,54273

Distancia promedio al centro del cluster 0,43925

Nombre	Media	Distancia	Máximo	Mínimo
X1	4,982	0,667	6,100	4,300
X2	1,706	0,620	2,500	0,500
X3	9,353	0,473	9,400	9,200
X4	6,082	0,862	6,300	4,800
X5	3,347	0,285	3,400	3,300
X6	3,371	0,778	4,000	2,800
X7	6,459	1,303	7,100	4,500

A partir de este momento, este análisis se reiteraría para el resto de clusters. En nuestro caso serían 5 salidas como ésta. Finalizaría el análisis con el análisis de la varianza para el conjunto, para comprobar la significatividad de las diferencias.

Análisis de varianza

Nombre	Media total	Desviación típica	Cuadrados medios entre	Cuadrados medios intra	Prueba F	Probabilidad
X1	3,515	1,314	15,258	0,410	37,199	0,00000
X2	2,364	1,190	17,131	0,331	51,707	0,00000
X3	7,894	1,380	13,601	0,480	28,336	0,00000
X4	5,278	1,119	12,877	0,510	25,226	0,00000
X5	2,946	0,812	11,731	0,559	20,995	0,00000
X6	2,665	0,767	10,721	0,601	17,833	0,00000
X7	6,971	1,577	13,277	0,494	26,897	0,00000

Matriz de distancias entre los centros de los clusters

Nombre	Cluster 1	Cluster 2	Cluster 3	Cluster 4	Cluster 5
Cluster 1	0,43925	1,90895	0,94355	1,35668	1,56228
Cluster 2	1,90895	0,38876	1,16415	0,64289	1,11596
Cluster 3	0,94355	1,16415	0,48482	2,02411	2,14762
Cluster 4	1,35668	0,64289	2,02411	0,15730	0,76806
Cluster 5	1,56228	1,11596	2,14762	0,76806	0,62190

Número de iteraciones: 2

Los elementos diagonales contienen la distancia media interna del cluster

Los elementos subdiagonales contienen las distancias entre clusters

Clusters finales

	X1	X2	X3	X4	X5	X6	X7
1	4,982	1,706	9,353	6,082	3,347	3,371	6,459
2	2,088	2,592	7,064	4,968	2,312	2,472	8,196
3	4,115	1,461	8,630	4,382	2,752	2,115	5,561
4	2,567	2,567	6,867	6,750	2,600	3,467	8,133
5	3,337	4,158	6,726	6,058	3,868	2,989	7,900

Se ha creado la variable GRUPOS_5

Análisis de los centros por medio de una tabulación de estadísticos

	Total	GRUPOS_5(Total)
Frecuencias		Subtotal	Grupo 1	Grupo 2	Grupo 3	Grupo 4	Grupo 5
Total	100	100	17	25	33	6	19
Velocidad de entrega
X1
Media	3,52	3,52	4,98	2,09	4,12	2,57	3,34
Desviación	1,32	1,32	0,69	0,82	0,99	0,68	0,75

Nivel de precio
X2
Media	2,36	2,36	1,71	2,59	1,46	2,57	4,16
Desviación	1,2	1,2	0,64	0,86	0,63	0,39	0,61

Flexibilidad en precios
X3
Media	7,89	7,89	9,35	7,06	8,63	6,87	6,73
Desviación	1,39	1,39	0,49	0,97	0,82	0,72	1,42

Imagen del fabricante
X4
Media	5,28	5,28	6,08	4,97	4,38	6,75	6,06
Desviación	1,12	1,12	0,89	0,57	0,85	0,27	0,97

Nivel de servicio
X5
Media	2,95	2,95	3,35	2,31	2,75	2,6	3,87
Desviación	0,82	0,82	0,29	0,63	0,69	0,26	0,69

Imagen del personal de ventas
X6
Media	2,66	2,66	3,37	2,47	2,12	3,47	2,99
Desviación	0,77	0,77	0,8	0,34	0,58	0,54	0,68

Calidad del producto
X7
Media	6,97	6,97	6,46	8,2	5,56	8,13	7,9
Desviación	1,59	1,59	1,34	0,96	1,04	0,28	1,31

Podemos también verificar el análisis realizado, con una prueba T que nos muestra las diferencias en medias de los grupos

	Total	GRUPOS_5(Total)
Frecuencias		(A) Subtotal	(B) Grupo 1	(C) Grupo 2	(D) Grupo 3	(E) Grupo 4	(F) Grupo 5
Total	100	100	17	25	33	6	19
Velocidad de entrega
X1	100	100	17	25	33	6	19
Casos válidos	100	100	17	25	33	6	19
Media	3,52	3,52 CE	4,98 ACDEF	2,09	4,12 aCEF	2,57	3,34 Ce
Desviación	1,32	1,32	0,69	0,82	0,99	0,68	0,75
Nivel de precio
X2	100	100	17	25	33	6	19
Casos válidos	100	100	17	25	33	6	19
Media	2,36	2,36 BD	1,71	2,59 BD	1,46	2,57 BD	4,16 ABCDE
Desviación	1,2	1,2	0,64	0,86	0,63	0,39	0,61
Flexibilidad en precios
X3	100	100	17	25	33	6	19
Casos válidos	100	100	17	25	33	6	19
Media	7,89	7,89 CEF	9,35 ACDEF	7,06	8,63 ACEF	6,87	6,73
Desviación	1,39	1,39	0,49	0,97	0,82	0,72	1,42
Imagen del fabricante
X4	100	100	17	25	33	6	19
Casos válidos	100	100	17	25	33	6	19
Media	5,28	5,28 D	6,08 ACD	4,97 D	4,38	6,75 AbCDf	6,06 ACD
Desviación	1,12	1,12	0,89	0,57	0,85	0,27	0,97
Nivel de servicio
X5	100	100	17	25	33	6	19
Casos válidos	100	100	17	25	33	6	19
Media	2,95	2,95 Ce	3,35 ACDE	2,31	2,75 c	2,6	3,87 ABCDE
Desviación	0,82	0,82	0,29	0,63	0,69	0,26	0,69
Imagen del personal de ventas
X6	100	100	17	25	33	6	19
Casos válidos	100	100	17	25	33	6	19
Media	2,66	2,66 D	3,37 ACD	2,47 d	2,12	3,47 ACD	2,99 CD
Desviación	0,77	0,77	0,8	0,34	0,58	0,54	0,68
Calidad del producto
X7	100	100	17	25	33	6	19
Casos válidos	100	100	17	25	33	6	19
Media	6,97	6,97 D	6,46 d	8,20 ABD	5,56	8,13 ABD	7,90 aBD
Desviación	1,59	1,59	1,34	0,96	1,04	0,28	1,31