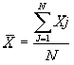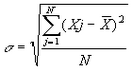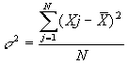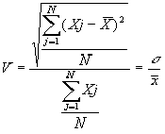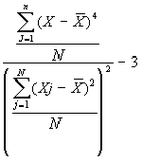Descriptivo

Media aritmética

Medida de tendencia central paramétrica, aplicable específicamente en el caso de variables cuantitativas con escalas de intervalo o de razón, que representa el punto de la distribución de los valores de una variable, en el que se hacen iguales las desviaciones en relación con dicho punto, de los valores de la distribución situados sobre ese punto con los situados por debajo de ese punto.

Mediana

Valor que deja el 50% de los casos de la distribución por arriba y por abajo del mismo. Si no existe valor exacto, siempre toma aquel valor que se acerca más al 50%

Primer cuartil

Valor que deja el 25% de los casos por detrás y el 75% de los casos por delante en la distribución. Si no existe valor exacto, siempre toma aquel valor que se acerca más al 25%

Tercer cuartil

Valor que deja el 75% de los casos por detrás y el 25% de los casos por delante en la distribución. Si no existe valor exacto, siempre toma aquel valor que se acerca más al 75%

Moda

Valor más repetido en la distribución; si hay varias modas, aparece un botón para desplegar la lista de modas.

Suma de casos

Agregación de los casos de la distribución

Máximo

Valor más alto de la distribución

Mínimo

Valor más bajo de la distribución

Rango

Diferencia entre el máximo y el mínimo

Desviación típica

Medida de dispersión paramétrica igual a la raíz cuadrada de la varianza, o de la media del cuadrado de las desviaciones de los valores de una distribución desde su media. Exige para ser válido su valor, por su condición de estadístico paramétrico, que la variable se distribuya normalmente y que esté medida por intervalos (métrico).

Varianza

Medida de dispersión paramétrica igual a la media del cuadrado de las desviaciones de los valores de una distribución desde su media. Exige para ser válido su valor por su condición de estadístico paramétrico, que la variable se distribuya normalmente y que esté medida por intervalos (métrico)

Coeficiente de variación

Dispersión relativa que se pueda dar en una distribución de frecuencias. Al ser un cociente adimensionado, puede servir como medida de comparación de dos distribuciones con media y desviaciones diferentes.

Error estimado para la media

Error que se comete con la media muestral sobre el verdadero valor poblacional.

Intervalo de confianza de la media

Si N es mayor que 30

Si N es menor que 30

Intervalo de confianza sobre la media. En ese intervalo de confianza se encuentra con un 95.5 % de confianza el verdadero valor poblacional de la media.

Coeficiente de asimetría

Coeficiente de sesgo cuartílico. Mide el nivel de simetría de la distribución respecto al valor central de la misma

Coeficiente de aplanamiento

Grado de apuntamiento de la curva normal. La constante 3 en la fórmula de la curtosis en la curva normal, tiene la misión de igualar a 0 el valor de la misma de forma que sea más fácil la interpretación. Valores inferiores a 0 implican una curva platicúrtica (aplanada) y valores superiores a 0 implican una curva leptocúrtica (apuntada).