Otro contraste es el que se realiza de la misma forma anterior, es decir sobre muestras consideradas independientes, pero tomando como estadístico a comparar la media, por tanto más adecuado para comparar mediciones que provienen de variables con escala de intervalo o métrica. En este caso la fórmula utilizada es:
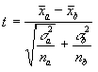
| • | xa es la media de la variable de filas para la alternativa a de la variable de columna |
| • | xb es la media de la variable de filas para la alternativa b de la variable de columna |
| • | na es el número de casos que han contribuido para el cálculo de la media en la alternativa a |
| • | nb es el número de casos que han contribuido para el cálculo de la media en la alternativa b |
| • | sa es la desviación típica de la variable de filas para la alternativa a |
| • | sb es la desviación típica de la variable de filas para la alternativa b |
Proceso de cálculo
Fichero > Prueba t para medias y porcentajes MI.gbw
Órdenes > Tabulación - > Tabulación de frecuencias - > GRP_EXP en columnas - > Variable VALOR en filas
Imaginemos que en un curso se ha hecho una explicación diferente de la situación política inestable que se vive en un país democrático en tres grupos diferentes dentro del curso. A posteriori de las charlas, se recoge una puntuación de la valoración que los individuos realizan sobre la situación política.
Recogemos los valores medios de los tres grupos y aplicamos la prueba t de Student.
Órdenes > Resultado de la tabulación - > Calcular estadísticos de frecuencias - > Pruebas de significación - > Prueba de significación: t - Student - > Intervalos 95 - 99% - > Columna de variable
El objetivo de esta técnica, es analizar si existen diferencias entre los distintos grupos experimentales, es decir, buscamos conocer si el tipo de explicación ha provocado diferencias en media aritmética en los distintos subgrupos maestrales.
Aplicamos el contraste t, derivado de la tabla de contingencia siguiente:
|
TOTAL |
GRP_EXP |
|
|
|---|---|---|---|---|
% Verticales |
|
(A) A1 |
(B) A2 |
(C) A3 |
TOTAL |
18 |
8 |
6 |
4 |
Medición de los efectos del estímulo |
|
|
|
|
VALOR |
18 |
8 |
6 |
4 |
Casos válidos |
100.0 |
100.0 |
100.0 |
100.0 |
NS/NC |
0.0 |
0.0 |
0.0 |
0.0 |
|
|
|
|
|
Media |
5.944 |
5.125 |
7.833 ac |
4.750 |
Desviación |
2.415 |
1.691 |
2.409 |
1.920 |
Observamos como resultado de la prueba que existen diferencias significativas entre el grupo A2 (denominado B en la prueba) y los grupos A1 y A3 (denominados como A y C respectivamente). Sabemos que las medias de las valoraciones son significativamente diferentes en la población de referencia (estimamos) porque aparecen en la prueba marcadas. Si observamos el la columna B vemos que en ella aparecen las letras a (representando la columna A o lo que es lo mismo el grupo A1) y c bajo la media de A2 (representando a la columna C o lo que es lo mismo: A3), cuyo valor es 7,833. Esa es la marca utilizada para mostrar las diferencias.
Por otro lado sabemos que esas diferencias lo son al 95% de confianza, pues aparecen en minúsculas. La prueba siempre muestra la significación en minúsculas para el límite inferior del intervalo los niveles de confianza que solicitamos par la prueba (observemos en el proceso que elegimos 95 - 99), por lo que 95 se mostrará en minúsculas y 99 se mostraría en mayúsculas.
Cabe por último reseñar, la simetría de la prueba t. Si A2 presenta diferencias positivas (el valor de t es positivo) con A1, A1 las presenta con A2 con signo negativo. La prueba sólo muestra los valores en las columnas que tienen las diferencias significativas positivas. De esta forma no se embarulla la información, repitiendo la misma en la tabla. En este tipo de pruebas se realizan tantos prueba t como parejas de grupos dividido por 2 existen.
Desde la versión 1344, se incorpora una modificación a la formulación anterior, incorporando nuevos conceptos como es el overlapping o solapamiento de muestras que ayuda a una mejor integración en la formulación de la restricción de grupos independientes en el contraste. El overlapping puede aplicarse o no desde el diálogo de pruebas de significación, así como la corrección de continuidad o la consideración de varianzas iguales. Como se puede observar en el diálogo por defecto aparece marcada la consideración de varianzas iguales u la aplicación del overlapping.
Se introduce un nuevo concepto que es la base efectiva. La base efectiva es el número de casos en solapamiento entre los grupos de las columnas (o filas) comparadas. La base efectiva se computa como un cociente entre la suma de pesos de los.
Su formulación para cada columna es
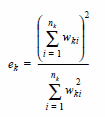
y para el total
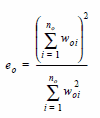 .
.
El test T para medias compara los valores de las medias en dos columnas de la tabla (columnas de códigos o subtotal de variable). Para cada dos columnas, estaremos testando que la diferencia entre las medias es 0, o dicho de otra forma que las medias son iguales.
La varianza es calculada como
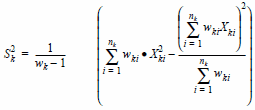
asumiendo que las muestras son extraídas de la misma población. Como no conocemos el valor poblacional de la varianza, asumimos la siguiente formulación
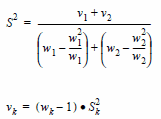
donde en el caso de datos no ponderados, se reduce a
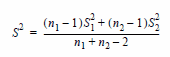
En el caso de no existir overlapping y n1 y n2 > 30
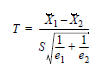
t es distiribuida con e1+e2-1 grados de libertad. Si existe overlapping, esta formulación ha de ser ajustada a
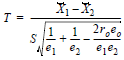
donde t sería distribuida con e1+e2-e0-1 grados de libertad y donde el coeficiente de correlación será
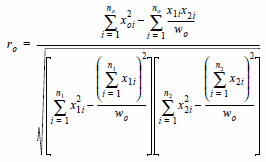
siendo
![]()