Prueba jhi2

 Top  Previous  Next

El índice jhi2 de Pearson es una prueba estadística no paramétrica, que compara las frecuencias realmente obtenidas con las frecuencias esperadas que son las que corresponderían a cada casilla de la tabla si su valor se ajustase a cualquier norma teórica previamente adoptada; en nuestro caso, una distribución proporcional de frecuencias normales. En definitiva, “se está calculando un índice acerca de la distancia entre lo real y lo esperado” (Manzano, 1995).

El valor numérico se obtiene como:

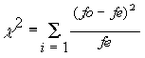
•fo, serán las frecuencias observadas en el experimento o muestra
•fe, serán las frecuencias esperadas teóricamente, se calculan con ...

•fo, serán las frecuencias observadas en el experimento o muestra
•fe, serán las frecuencias esperadas teóricamente
•N, es el número de efectivos muestrales

Esta prueba se suele utilizar (entre muchas otras posibilidades) para contrastar la hipótesis nula que los resultados obtenidos de una muestra no son significativos con relación a la población total, o bien como prueba de independencia para comprobar la existencia o no de asociación entre las variables. En este caso, la prueba indica la existencia de asociación pero no la cuantifica.

Proceso de cálculo

Fichero> Datos bivariante.gbw

Órdenes > Análisis - > Pruebas de asociación - > Prueba c2 de tabla - > Seleccionar en columnas la variable Edad y en filas la variable P10.

Observada
Esperada
jhi² Pearson

 

- 25

- 35

- 45

- 55

+55

 

348

116

96

60

40

36

Corolla Verso

52

16
17
0.06

16
14
0.29

4
9
2.78

8
6
0.67

8
5
1.80

Megane Scenic

44

16
15
0.07

8
12
1.33

4
8
2.00

12
5
9.80

4
5
0.20

Peugeot 307 Toruing

200

60
67
0.73

52
55
0.16

40
34
1.06

24
23
0.04

24
21
0.43

Otros Renault Space

40

4
13
6.23

20
11
7.36

4
7
1.29

4
5
0.20

8
4
4.00

Xsara Picasso

124

48
41
1.20

44
34
2.94

12
21
3.86

12
14
0.29

8
13
1.92

Volkswagen Sharan

24

4
8
2.00

8
7
0.14

8
4
4.00

4
3
0.33

0
2
2.00

Volkswagen Touran

48

24
16
4.00

8
13
1.92

8
8
0.00

4
6
0.67

4
5
0.20

Chrysler Grand Voyager

16

0
5
5.00

8
4
4.00

8
3
8.33

0
2
2.00

0
2
2.00

Otros Opel Zafira

16

0
5
5.00

4
4
0.00

4
3
0.33

4
2
2.00

4
2
2.00

Seat Alhambra

8

4
3
0.33

4
2
2.00

0
1
1.00

0
1
1.00

0
1
1.00

Otros

132

32
44
3.27

52
36
7.11

36
23
7.35

8
15
3.27

4
14
7.14

Jhi² Pearson = 130.10

Grados de libertad = 40

Significación = 0.00

En esta tabla de frecuencias reflejamos la información de la frecuencia observada en la muestra, la frecuencia que cabría esperar si se mantuvieran las distribuciones marginales, y por último el valor de c2 para cada una de las celdas de la tabla.

Al final de la tabla, aparece el estadístico jhi² de Pearson. Como la H0 que establecemos es la independencia o no relación de las variables, deberemos rechazar la misma, y aceptar la Ha, pues la significación es menor a 0,0450 (@ 0,05). Este valor se toma pensando en nivel de confianza del 95,45%, pero podemos ser más rígidos y rebajar el punto crítico hasta un nivel de significación de 0,0022 y estaríamos trabajando con un nivel de confianza del 99,78%.

Debemos concluir, por tanto, que existe una relación de dependencia entre las distintas categorías de edad y los recuerdos de marca espontánea en los vehículos de fines de semana. El investigador deberá trazar una relación entre ambas variables y deberá buscar los estímulos o factores que provocan o han provocado en esa muestra (y por ende en la población) esa asociación.

Para Manzano (1995) jhi2 es una prueba de aproximación, no exacta, y presenta una serie de limitaciones:

•Es una técnica de aproximación, no exacta. Por ello, a menor muestra, más pequeño debe ser el nivel de significación para tomar la decisión con relativa seguridad.
•En esencia, la prueba parte de una utilización de variables continuas, sin embargo se utiliza con variables nominales, lo cual genera una incorrección, que sólo es insalvable en las tablas de 2x2, donde se utiliza la corrección por continuidad de Yates.
•Es una prueba que depende de la unidad de medida, efecto que salvan otras pruebas como V de Cramer.
•La disparidad entre la aproximación de Pearson y la distribución c aumenta conforme disminuye N. Utilizar probabilidad exacta de Fisher si hay frecuencias menores a 5.
•El modelo puede no funcionar correctamente cuando existen frecuencias esperadas inferiores a 5. Se considera válido si menos del 20% de las celdas tienen frecuencias esperadas inferiores a 5. Caso de no ser así, no queda más remedio que agrupar categorías columna o fila.