Descripción de la técnica
Paradigma de las técnicas de dependencia y base de una gran parte de las técnicas multivariantes, su objetivo es explicar el comportamiento de una variable dependiente a partir de las relaciones entre variables independientes. Trata de captar los efectos de cada variable por separado. Analizamos sólo OLS (mínimos cuadrados ordinarios).
Grado de utilización en la práctica
En desuso como tal, porque se está modelizando hoy en día con evoluciones o especificaciones del mismo: logit, probit, logística, etc. aunque sigue siendo la base de todo el resto de análisis; análisis tan “famosos” como el factorial o el multinomial logit tiene detrás modelos de regresión lineal.
Condiciones para el análisis
Las variables con las que se realiza el análisis deben ser de tipo métrico. Si por alguna razón se quisiera introducir alguna variable de tipo no métrico, se debería binarizar e introducir tantas variable de tipo 0/1 como categorías tuviera esa variable nominal (o sólo algunas de ellas). El modelo que se va a establecer será de tipo lineal. Otras características que se piden son:
| • | homocedasticidad |
| • | ausencia de correlación serial |
| • | ausencia de multicolinealidad |
| • | matriz de datos no estocástica e independiente |
El modelo utilizado es el paso a paso (forward stepwise). En este tipo de metodología, las variables se incorporan una a una, comenzado por aquella que tiene un mayor poder explicativo de la variable dependiente. Se puede combinar con una metodología de forzado de participación (enter).
Suma de cuadrados explicada por la variable actual |
Total de la varianza explicada por el modelo que aporta la variable que se introduce en el paso n |
|---|---|
R cuadrado de la variable |
% de la varianza explicada por el modelo que aporta la variable que se introduce en el paso n |
Suma de cuadrados explicada por las variables (acumulado) |
Total de la varianza explicada por el modelo que aportan las variables introducidas en el modelo hasta el paso n |
R cuadrado de las variables (acumulado) |
% de la varianza explicada por el modelo que aportan las variables introducidas en el modelo hasta el paso n |
Suma de cuadrados total |
Total de la varianza explicada por el modelo que aportan las variables introducidas al final del modelo. |
Coeficiente de correlación múltiple y coeficiente de correlación múltiple ajustado a los grados de libertad |
Bondad del ajuste producido por la totalidad del modelo |
Valor F para el análisis de varianza y significación |
Prueba inferencial que aporta la significatividad de la relación lineal planteada en el conjunto del modelo. |
Error estándar de estimación y error estándar de estimación ajustado a los grados de libertad |
Estimación del error que se produce en el modelo |
Predicción por el modelo |
Valor de la variable dependiente utilizando el modelo lineal de regresión |
Residuo |
Diferencia entre el valor real y el predicho por el modelo |
Coeficiente de regresión |
Valor que permite medir la relación de la variable independiente con la dependiente del modelo. |
Error estándar de regresión |
Medida de precisión de los coeficientes de regresión proporcional al error de estimación e inversamente proporcional a la variabilidad de la variable, descontada la del resto de variables del modelo. |
Valor t-Student y significación |
Prueba inferencial que aporta la significatividad de la relación lineal planteada específicamente para el regresor especificado |
Proceso de cálculo
Fichero Datos para regresión múltiple
Órdenes Análisis > Regresión > Múltiple
Variables Dependiente TAD (tensión arterial)
Variables Independientes COLESTEROL, IMC (índice masa corporal) y EDAD
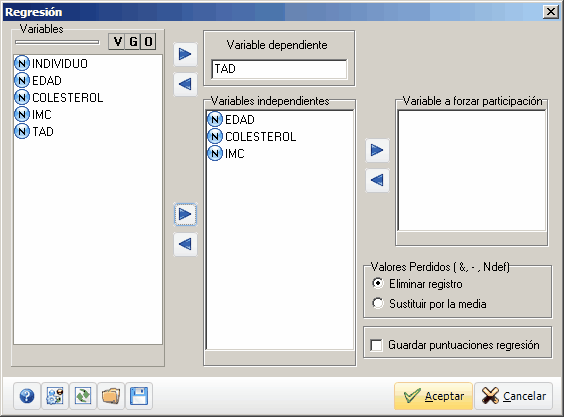
Variables analizadas: TAD COLESTEROL IMC EDAD
Estadísticos
Número de casos=67
Número de variables=4
Constante límite=0,00000
Nombre de la variable |
Media aritmética |
Desviación típica |
TAD |
81,40299 |
11,36590 |
COLESTEROL |
236,26866 |
34,03723 |
IMC |
25,53567 |
3,95674 |
EDAD |
55,04478 |
7,16776 |
|
TAD |
COLESTEROL |
IMC |
EDAD |
|---|---|---|---|---|
TAD |
1,00000 |
0,69066 |
0,56117 |
0,37490 |
COLESTEROL |
0,69066 |
1,00000 |
0,55787 |
0,31954 |
IMC |
0,56117 |
0,55787 |
1,00000 |
0,25647 |
EDAD |
0,37490 |
0,31954 |
0,25647 |
1,00000 |
La primera información que se ofrece son los estadísticos básicos de las variables que participan en el análisis y su matriz de coeficientes de correlación de Pearson. Para analizar la significación de cada coeficiente, más allá de lo meramente visual, deberemos acudir a realizar una matriz de coeficientes de correlación según lo visto en el capítulo anterior.
Variable incluida |
COLESTEROL |
|
Variable forzada |
Suma de cuadrados explicada por variable |
4067,11231 |
R² (proporción explicada por variable) |
0,47702 |
Suma de cuadrados explicada por todas variables |
4067,11231 |
R² (proporción explicada por todas variables) |
0,47702 |
Suma de cuadrados total |
8526,11940 |
Coeficiente de correlación múltiple |
0,69066 |
Coeficiente de correlación múltiple ajustado |
0,69066 |
Valor F para el análisis de varianza |
59,28726 |
Significación |
0,00000 |
Error estándar de estimación |
8,28252 |
Error estándar de estimación ajustado |
8,28252 |
Variable |
Coeficiente de regresión |
Error estándar de regresión |
Valor t-Student calculado |
Significación |
COLESTEROL |
0,23063 |
0,02995 |
7,69982 |
0,00000 |
Constante |
26,91220 |
|
|
|
En el primer paso, se encuentra que la variable más explicativa de la TAD es el COLESTEROL. Se ofrecen sus resultados y vemos que el modelo arroja un coeficiente de determinación de 0,477. Este coeficiente se irá modificando a medida que se incorporen nuevas variables.
Variable incluida |
IMC |
|
Variable forzada |
Suma de cuadrados explicada por variable |
382,87474 |
R² (proporción explicada por variable) |
0,04491 |
Suma de cuadrados explicada por todas variables |
4449,98705 |
R² (proporción explicada por todas variables) |
0,52192 |
Suma de cuadrados total |
8526,11940 |
Coeficiente de correlación múltiple |
0,72244 |
Coeficiente de correlación múltiple ajustado |
0,72798 |
Valor F para el análisis de varianza |
34,93498 |
Significación |
0,00000 |
Error estándar de estimación |
7,98057 |
Error estándar de estimación ajustado |
8,04173 |
Variable |
Coeficiente de regresión |
Error estándar de regresión |
Valor t-Student calculado |
Significación |
COLESTEROL |
0,18306 |
0,03478 |
5,26427 |
0,00000 |
IMC |
0,73346 |
0,29915 |
2,45185 |
0,01621 |
Constante |
19,42100 |
|
|
|
En este paso 2, se introduce el IMC, denotando que el modelo mejora muy poco, pues su R2 sube hasta el 0,521. Observamos que la aportación de la variable al modelo es bien poca, 0,044.
Variable incluida |
EDAD |
|
|
Suma de cuadrados explicada por variable |
172,81718 |
R² (proporción explicada por variable) |
0,02027 |
Suma de cuadrados explicada por todas variables |
4622,80423 |
R² (proporción explicada por todas variables) |
0,54219 |
Suma de cuadrados total |
8526,11940 |
Coeficiente de correlación múltiple |
0,73634 |
Coeficiente de correlación múltiple ajustado |
0,74775 |
Valor F para el análisis de varianza |
24,87088 |
Significación |
0,00000 |
Error estándar de estimación |
7,87130 |
Error estándar de estimación ajustado |
7,99334 |
Variable |
Coeficiente de regresión |
Error estándar de regresión |
Valor t-Student calculado |
Significación |
COLESTEROL |
0,17015 |
0,03516 |
4,83922 |
0,00002 |
IMC |
0,68421 |
0,29652 |
2,30747 |
0,02310 |
EDAD |
0,23943 |
0,14336 |
1,67012 |
0,09590 |
Constante |
10,55111 |
|
|
|
Se han creado 2 nuevas variables en el estudio que contienen los datos de la tabla residual con los valores predichos y los residuos de la variable dependiente que se han obtenido tras la regresión.
Por último, se añade la EDAD, que al igual que la variable anterior, no aporta tampoco mucho. En definitiva, obtenemos un modelo, en el que COLESTEROL e IMC son significativos, no EDAD (significación de t con un 0,09).