Prueba muy conocida y utilizada que permite reducir el espacio dimensional de un conjunto multivariante de datos a un conjunto de factores cuya composición proviene de combinaciones lineales y normales que maximizan la representatividad de los datos originales y minimizan la pérdida de información. En la práctica permite reducir y agrupar el número de dimensiones de un problema. Se analiza en este proceso el total de la varianza de las variables que intervienen en el análisis, a diferencia del análisis factorial que sólo analiza la varianza común. “Es el método más autilizado en marketing y corresponde a una aproximación empírica en la cual se busca extraer factores, combinación lineal de las variables iniciales” (Pedret, Sagnier yCamp:98).
Este análisis factorial es muy utilizado en la práctica. Tiene una infinidad de variantes, pero sin duda la más utilizada es la del análisis factorial de componentes principales. Estas variantes son presentadas para estructuras de datos específicos: componentes principales, máxima verosimilitud, alpha, etc.…
El objetivo del análisis es la reducción del conjunto de datos que disponemos, en una menor cantidad de información opero con un mayor de representación. El objetivo es resumir para comprender. El máximo número de componentes a obtener es igual al número de variables originales incluidas en la estructura de datos, aunque retendremos sólo las más trascendentes.
La situación ideal en este análisis sería la de pocos componentes que explicaran mucha varianza; en el proceso de análisis surgen los denominados, pesos, saturaciones o cargas que son el peso de la variable en cada componente o factor. El ideal es que cada variable tenga saturaciones altas en un único factor y bajas en el resto.
Con una gran habitualidad, se analizan los datos de la solución rotada, dado que suele explicar la realidad mejor que la solución directa. La rotación más típica es la rotación ortogonal VARIMAX, pues intenta maximizar la correlación en sentido positivo/negativo de las variables y minimizar el de otras, haciendo por tanto más evidentes las cargas factoriales extremas en el análisis.
Para poder utilizar este análisis:
| • | Variables con escala al menos de intervalo. |
| • | Matriz de individuos por variables. |
| • | Correlaciones significativas entre las variables que participan. Se comparte las mismas fuentes de variabilidad, es decir que las correlaciones sean elevadas. |
Información ofrecida en el análisis de componentes principales
Matriz de correlaciones |
Matriz que nos permite observar a simple vista los coeficientes de correlación de Pearson entre las variables que intervienen en el análisis. |
|---|---|
Prueba de esfericidad de Bartlett |
Prueba que reafirma la viabilidad del análisis de componentes principales, pues testa que la matriz de correlaciones es significativamente diferente de la matriz identidad. En este caso, la nube de puntos sería una esfera. Se obtiene un valor de c² que si es significativo, se rechaza la hipótesis nula de esfericidad o incorrelación. |
Valor propio |
Este valor indica la varianza de la matriz de correlaciones explicada por el componente o factor. Suma de los cuadrados de las saturaciones de cada variable en cada componente o factor. Al igual que en anaco, diremos que es la cantidad de varianza del modelo que explica cada componente o factor. |
Solución directa |
Matriz de pesos factoriales donde se puede observar la participación o peso de cada variable en el componente |
Solución rotada |
Matriz de pesos factoriales donde se puede observar la participación o peso de cada variable en el componente tras la rotación de los ejes factoriales. |
Contribuciones absolutas |
Cada celda muestra el porcentaje de participación de cada variable en el componente extraído. El porcentaje es vertical, la suma de la columna es 100. |
Contribuciones relativas |
(1) La primera fila de valores muestra el porcentaje de participación de cada variable en los diferentes factores extraídos y por tanto suma 100.(2) La segunda fila de valores muestra el porcentaje de participación de cada variable en los diferentes factores, contabilizando los extraídos y los no extraídos. |
Comunalidad final |
Proporción de la varianza inicial de una variable explicada por el componente o factor. Suma de los cuadrados de las saturaciones de una variable en todos los factores. |
Rotación |
Método matemático utilizado para rotarlos ejes factoriales y facilitar el análisis de los investigadores. En BarbWin se utiliza VARIMAX que tiende a maximizar la suma de las varianza de los componentes, por lo que implica que cada variable cargue mucho en un componente y poco en el resto. El método de componentes principales extrae componentes con baja correlación. |
Proceso de cálculo
Fichero Datos para componentes.gbw
Órdenes Análisis > Reducción de datos > Componentes principales
Variables Todas (C1 a C7)
Opciones Defecto. Guardar puntuaciones factoriales.
Cálculo de un análisis de componentes principales
Número de sujetos 25
Número de variables 7
Número máximo de iteraciones 51
Número de iteraciones realizadas 7
Se han creado 3 nuevas variables en el estudio
Estas variables contienen las puntuaciones de los factores
Variables analizadas: C1 C2 C3 C4 C5 C6 C7
Descriptivos
Variable |
Media |
Desviación típica |
C1 |
4,32 |
1,86 |
C2 |
4,04 |
1,86 |
C3 |
3,96 |
1,79 |
C4 |
3,92 |
1,80 |
C5 |
3,84 |
1,93 |
C6 |
4,16 |
1,84 |
C7 |
4,24 |
1,88 |
Correlaciones en un análisis de componentes principales
|
C1 |
C2 |
C3 |
C4 |
C5 |
C6 |
C7 |
C1 |
1,00000 |
-0,00385 |
0,62794 |
0,08239 |
0,67493 |
-0,10049 |
-0,30858 |
C2 |
-0,00385 |
1,00000 |
0,15068 |
-0,24789 |
0,04832 |
0,58231 |
-0,22971 |
C3 |
0,62794 |
0,15068 |
1,00000 |
-0,18192 |
0,48041 |
0,09048 |
-0,57964 |
C4 |
0,08239 |
-0,24789 |
-0,18192 |
1,00000 |
0,27194 |
0,01659 |
0,47430 |
C5 |
0,67493 |
0,04832 |
0,48041 |
0,27194 |
1,00000 |
-0,10977 |
-0,05798 |
C6 |
-0,10049 |
0,58231 |
0,09048 |
0,01659 |
-0,10977 |
1,00000 |
0,02459 |
C7 |
-0,30858 |
-0,22971 |
-0,57964 |
0,47430 |
-0,05798 |
0,02459 |
1,00000 |
Correlaciones máximas en un análisis de componentes principales
|
Coeficiente de correlación |
Variables |
Significación |
|---|---|---|---|
1 |
0,67493 |
C1- C5 |
0,00013 |
2 |
0,62794 |
C1- C3 |
0,00043 |
3 |
0,58231 |
C2- C6 |
0,00116 |
4 |
-0,57964 |
C3- C7 |
0,00123 |
5 |
0,48041 |
C3- C5 |
0,00724 |
6 |
0,47430 |
C4- C7 |
0,00796 |
7 |
-0,30858 |
C1- C7 |
0,06489 |
8 |
0,27194 |
C4- C5 |
0,09281 |
9 |
-0,24789 |
C2- C4 |
0,11524 |
10 |
-0,22971 |
C2- C7 |
0,13444 |
11 |
-0,18192 |
C3- C4 |
0,19395 |
12 |
0,15068 |
C2- C3 |
0,23922 |
13 |
-0,10977 |
C5- C6 |
0,30365 |
14 |
-0,10049 |
C1- C6 |
0,31874 |
15 |
0,09048 |
C3- C6 |
0,33514 |
16 |
0,08239 |
C1- C4 |
0,34849 |
17 |
-0,05798 |
C5- C7 |
0,38968 |
18 |
0,04832 |
C2- C5 |
0,40669 |
19 |
0,02459 |
C6- C7 |
0,45154 |
20 |
0,01659 |
C4- C6 |
0,46754 |
21 |
-0,00385 |
C1- C2 |
0,49143 |
Prueba de esfericidad de Bartlett
|
Resultado |
Determinante de la matriz de correlaciones |
0,06287 |
Prueba de esfericidad de Bartlett |
57,64 |
Significación |
0,00003 |
Grados de libertad |
21 |
“La prueba de esfericidad de Barlett comprueba si la matriz de correlaciones es una matriz identidad” (Miquel, Bigné, Levy, Cuenca y Miquel:238). Podremos dar como válidos aquellos resultados que nos presenten un valor elevado del test y cuya significación sea menor que 0,05. Si es así, el análisis de componentes es adecuado para la estructura de datos analizada.
Valores propios en un ACP
|
Valores |
% Varianza explicada |
% Varianza acumulada |
Componente 1 |
2,45698 |
35,10 |
35,10 |
Componente 2 |
1,82300 |
26,04 |
61,14 |
Componente 3 |
1,35853 |
19,41 |
80,55 |
Componente 4 |
0,51524 |
7,36 |
87,91 |
Componente 5 |
0,37712 |
5,39 |
93,30 |
Componente 6 |
0,27748 |
3,96 |
97,26 |
Componente 7 |
0,19164 |
2,74 |
100,00 |
Solución directa
|
Componente 1 |
Componente 2 |
Componente 3 |
C1 |
0,81786 |
-0,37422 |
0,08789 |
C2 |
0,26713 |
0,70436 |
0,47785 |
C3 |
0,89059 |
0,03942 |
-0,04198 |
C4 |
-0,20051 |
-0,64600 |
0,57558 |
C5 |
0,66709 |
-0,50640 |
0,32468 |
C6 |
0,04196 |
0,59087 |
0,69846 |
C7 |
-0,66075 |
-0,40301 |
0,44289 |
Solución rotada [Método VARIMAX]
|
Componente 1 |
Componente 2 |
Componente 3 |
C1 |
0,89709 |
0,07991 |
-0,07422 |
C2 |
0,04792 |
0,22396 |
0,86218 |
C3 |
0,76202 |
0,44700 |
0,12641 |
C4 |
0,21473 |
-0,85974 |
-0,05947 |
C5 |
0,86974 |
-0,22387 |
-0,01725 |
C6 |
-0,05645 |
-0,09086 |
0,90955 |
C7 |
-0,32152 |
-0,82991 |
-0,05505 |
% Varianza explicada |
32,81 |
24,89 |
22,84 |
Contribuciones absolutas
|
Componente 1 |
Componente 2 |
Componente 3 |
C1 |
35,04 |
0,37 |
0,34 |
C2 |
0,10 |
2,88 |
46,49 |
C3 |
25,28 |
11,47 |
1,00 |
C4 |
2,01 |
42,42 |
0,22 |
C5 |
32,93 |
2,88 |
0,02 |
C6 |
0,14 |
0,47 |
51,74 |
C7 |
4,50 |
39,52 |
0,19 |
Contribuciones relativas
|
Componente 1 |
Componente 2 |
Componente 3 |
C1 |
98,54 |
0,78 |
0,67 |
C2 |
0,29 |
6,30 |
93,41 |
C3 |
72,91 |
25,09 |
2,01 |
C4 |
5,85 |
93,71 |
0,45 |
C5 |
93,75 |
6,21 |
0,04 |
C6 |
0,38 |
0,98 |
98,64 |
C7 |
13,00 |
86,62 |
0,38 |
Comunalidades
Variables |
Comunalidad |
|---|---|
C1 |
0,81666 |
C2 |
0,79582 |
C3 |
0,79647 |
C4 |
0,78881 |
C5 |
0,80687 |
C6 |
0,83873 |
C7 |
0,79516 |
Puntuaciones de factoriales de componentes
|
Componente 1 |
Componente 2 |
Componente 3 |
C1 |
0,39331 |
-0,01852 |
-0,04576 |
C2 |
0,01224 |
0,04648 |
0,53152 |
C3 |
0,30485 |
0,19447 |
0,04539 |
C4 |
0,16623 |
-0,53078 |
0,04868 |
C5 |
0,40678 |
-0,20521 |
0,02035 |
C6 |
-0,00788 |
-0,13958 |
0,59172 |
C7 |
-0,07571 |
-0,46895 |
0,04278 |
Nuestro análisis implicará el que analicemos la solución rotada, extrayendo la información de cada componente. Como norma general es aceptado el que en cada componente se extraigan las cargas que sean mayores, desde la más alta, hasta la que sea mayor que el 50% de la más alta, siempre y cuando alguna de éstas no esté cargando más en otro componente del sistema. En la ventana de información (no en resultados) BarbWin marca en color rojo la solución que considera adecuada.
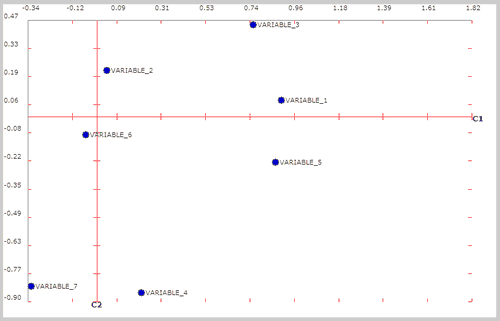
Las variables están mejor representadas cuanto más alejadas están del centro del gráfico.. En nuestro ejemplo gráfico, C2 y C6 no están muy bien representadas. Su calidad es muy mala ya que si nos damos cuenta, el gráfico corresponde a las coordenadas entre las componentes 1 y 2.
Gráfico de componentes
En muchas ocasiones, al guardar las puntuaciones factoriales, éstas se usan como entrada de datos para la realización de un cluster k-means con el objetivo de buscar grupos de casos, respecto a sus puntuaciones en los factores.